Lots is written on this blog about “Poststratification”. Andrew addresses it formally with a “Mister“. But when I learned it from Alan Zaslavsky’s course it was casually just “Poststratification”. At the time it sounded to me like damage control after we forgot to stratify.
- “Stratification” so that your sample has the same distribution for variables X as in the population: divide the population into strata (i.e. groups) based on X. Then take a sample in each stratum proportional to its size.
- “Post“: divide the population into strata only after the sample is already selected.
(As Raphael Nishimura and Andrew Gelman pointed out in the comments below, stratification has other uses !)
Fancy graphics from a DOL video I worked on:

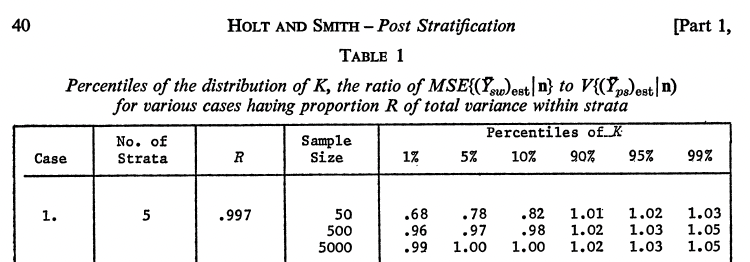
How can Poststratification help ?
Suppose we want to estimate E[Y], the population mean. But we only have Y in the survey sample. For example, suppose Y is voting Republican. We can use the sample mean, ybar = Ehat[Y | sample] (I don’t know how to LaTeX on this blog).
But our sample mean is conditional on being sampled. And what if survey-takers are more or less Republican than the population ? As Joe Blitzstein teaches us: “Conditioning is the soul of statistics.” Conditioning on being sampled might bias our estimate. But maybe more conditioning can also somehow help us ?! Joe taught me to try conditioning whenever I get stuck.

If we have population data on X, e.g. racial group, then we can estimate Republican vote share conditional on racial group E[Y|X] and aggregate according to the known distribution of racial groups, invoking the law of total expectation (Joe’s favorite): E[Y] = E[E[Y|X]]. So if our sample has the wrong distribution of racial groups, at least we fix that with some calibration. Replacing “E” with estimates “Ehat”, poststratification estimates E[Y] with E[Ehat[Y | X, sample]].
When our estimate of E[Y|X] is the sample mean of Y for folks with that X, the aggregate estimate is classical poststratification, yhat_PS. When our estimate of E[Y|X] is based on a model that regularizes across X, the aggregate estimate is Multilevel Regression (“Mister“) and Poststratification, yhat_MRP. Gelman 2007 shows how yhat_MRP is a shrinkage of yhat_PS towards ybar.
Which estimate is best for estimating E[Y] ? ybar, yhat_PS, or yhat_MRP ?
As Kuh et al 2023 write:
it is not individual predictions that need to be good, but rather the aggregations of these individual estimates.
A parallel approach is through simulation studies—for greater realism, these can often be constructed using subsamples of actual surveys—as well as theoretical studies of the bias and variance of poststratified estimates with moderate sample sizes.